Introduction
In this second post, we will take another step forward. We’ll dive into the concept of linear regression, explore its connection to neural networks, and demonstrate how to build a model from scratch. This approach will help us gain a deeper understanding of the core concepts behind both linear regression and neural networks.
Linear Regression
Model and Loss function
Before starting, we need to define some terminology. When we want to predict a value, we call it a label or target. Each label is associated with its own features. The model makes predictions based solely on these features. Therefore, we need to refine the model to accurately predict the correct label based on the provided input features.
We want to predict a target, $ \hat{y}$, based on a set of features grouped in a vector called ${X}$. To make the prediction, we need to find the weight vector ${W}$ and the bias $ B $ that give us the most accurate predictions. This relationship can be expressed using the dot product:
If we want to group everything together, we can define the X matrix, having along the lines the features of a single label, so we have the $\hat{y}$ vector that represents the vector of the prediction given the matrix features and the bias vector:
Now we need to define a loss function to evaluate the model. The most common is the squared error, where $\hat{y}_i$ is the prediction and $y_i$ is the corresponding true label.
We can observe that the loss is a function of weight and bias.
Now we can extend the evaluation of the loss along all the predictions, averaging it to obtain an intuitive idea of how our model is performing.
We have to keep in mind our goal: we want to find W and B that give us the minimum value of loss along all the predictions.
Minibatch Stochastic Gradient Descent
The key to optimizing a model and improving its predictions is to iteratively update the weights by modifying them in the opposite direction of the gradient of the loss function. This process is known as gradient descent. Although it may seem simple at first glance, it is the foundation of many advanced techniques in machine learning and plays a central role in training modern models.
To optimize the process, we do not update the model using the entire dataset at once. Instead, we randomly select smaller subsets of the data, called batches. The model is then optimized iteratively by performing updates on these batches, which makes the process more efficient and scalable, especially for large datasets. This approach is commonly referred to as mini-batch gradient descent.
To keep it simple we can break down this process into four steps:
- Batch Selection: Randomly choose a small subset of training data. This approach balances computational efficiency with learning effectiveness. Instead of processing the entire dataset, which would be slow and memory-intensive, we sample a representative mini-batch that captures the overall data characteristics.
- Loss Calculation: Measure how far the model’s predictions are from the true values for each example in the batch. Compute the average loss, which serves as a performance metric. This average loss quantifies the model’s current error, providing a clear signal about how well (or poorly) the model is performing on this particular set of examples.
- Gradient Computation: Calculate the derivative of the loss with respect to each model parameter. This gradient acts like a compass, pointing to the direction that would most quickly increase the loss. By understanding how each weight contributes to the model’s error, we can intelligently adjust the model’s internal representation to improve its predictive capabilities.
- Parameter Update: Move the model’s parameters in the opposite direction of the gradient, scaled by a small learning rate. This is akin to taking careful steps down a complex landscape, where each step aims to reduce the overall error. The learning rate determines the size of these steps – too large, and you might overshoot the optimal solution; too small, and progress becomes painfully slow.
If we want to express this in formulas we have:
1) The weights update:
2) The Bias Update:
Linear Regression as a Neural Network
While linear models are not sufficiently rich to express complex relationships between features, we can introduce neural networks to obtain a more expressive model. Nevertheless, we can also view a linear model as a neural network where every input feature corresponds to a neuron with its own weight and bias.
Implementation using object-oriented design
To gain a deeper understanding of how a model is created and trained, we aim to implement the classes and methods from scratch. We are following this approach because, in my opinion, using machine learning libraries like PyTorch directly does not provide a comprehensive understanding of what happens under the hood.
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import torch
Now we are ready to implement from scratch our model for linear regression, we need :
- The model
- The loss function
- The optimization algorithm
- The training function
Building the model
class LinearRegressionModel:
def __init__(self, num_inputs, learning_rate, sigma=0.01):
"""
Initialize the model parameters.
Args:
- num_inputs (int): Number of input features.
- learning_rate (float): Learning rate for gradient descent.
- sigma (float): Standard deviation for initializing weights.
"""
self.num_inputs = num_inputs
self.learning_rate = learning_rate
# Initialize weights and bias
self.w = torch.normal(mean=0.0, std=sigma, size=(num_inputs, 1), requires_grad=True)
self.b = torch.zeros(1, requires_grad=True)
Here we have created a class that contains the weights and bias. Additionally, we have introduced the hyperparameters, which are typically user-defined and used to adjust various aspects during the training phase. The weights are sampled from a normal distribution with a mean of 0 and a standard deviation of 0.01, while the bias is initialized to zero.
Now we can add the method to obtain the forward pass:
@add_to_class(LinearRegressionModel)
def forward(self, X):
"""
Compute the forward pass: y = Xw + b.
Args:
- X (torch.Tensor): Input tensor of shape (batch_size, num_inputs).
Returns:
- torch.Tensor: Predicted values of shape (batch_size, 1).
"""
return torch.matmul(X, self.w) + self.b
Building the loss function
Now we add the method to calculate the loss for a single batch of examples by using the squared loss function and then returning the mean.
@add_to_class(LinearRegressionModel)
def compute_loss(self, y_pred, y_true):
"""
Compute Mean Squared Error loss.
Args:
- y_pred (torch.Tensor): Predicted values.
- y_true (torch.Tensor): True values.
Returns:
- torch.Tensor: Scalar loss value.
"""
return 0.5 * ((y_pred - y_true) ** 2).mean()
Building the optimization algorithm
This is the fundamental part of our model—the algorithm that allows us to improve its predictions. We are going to implement Stochastic Gradient Descent (SGD), as discussed earlier.
The steps we want to follow are:
- Randomly select a batch from the training set.
- Make predictions using the selected batch.
- Compute the loss of the predictions.
- Calculate the gradient of the loss with respect to the weights and bias.
- Update the parameters (weights and bias) using the learning rate and computed gradients.
@add_to_class(LinearRegressionModel)
def update_parameters(self):
"""
Update the model parameters using gradient descent.
"""
with torch.no_grad():
self.w -= self.learning_rate * self.w.grad
self.b -= self.learning_rate * self.b.grad
# Manually zero the gradients
self.w.grad.zero_()
self.b.grad.zero_()
def train_step(self, X, y, batch_size):
"""
Perform a single training step.
Args:
- X (torch.Tensor): Input data of shape (num_samples, num_inputs).
- y (torch.Tensor): Target data of shape (num_samples, 1).
- batch_size (int): Number of samples per batch.
Returns:
- float: Loss value for the batch.
"""
# Sample a random batch
num_samples = X.shape[0]
indices = torch.randint(0, num_samples, (batch_size,))
X_batch = X[indices]
y_batch = y[indices]
# Forward pass
y_pred = self.forward(X_batch)
# Compute loss
loss = self.compute_loss(y_pred, y_batch)
# Backward pass
loss.backward()
# Update parameters
self.update_parameters()
# Return the loss value as a scalar
return loss.item()
Building the training method
The last step to complete our model is to implement a method that allows us to train it. It would be useful to visualize how the weights, bias, and learning rate change throughout the training process, so we can also add a method to plot this information.
@add_to_class(LinearRegressionModel)
def train(self, X, y, epochs, batch_size):
"""
Train the model over multiple epochs.
Args:
- X (torch.Tensor): Input data of shape (num_samples, num_inputs).
- y (torch.Tensor): Target data of shape (num_samples, 1).
- epochs (int): Number of training epochs.
- batch_size (int): Number of samples per batch.
Returns:
- list: List of loss values for each epoch.
"""
losses = []
for epoch in range(epochs):
# Perform a training step and compute the average loss for the epoch
loss = self.train_step(X, y, batch_size)
losses.append(loss)
# Print progress every 10 epochs
if epoch % 10 == 0:
print(f"Epoch {epoch}, Loss: {loss:.6f}")
return losses
Testing The model
Now that the class is built from scratch, we can proceed with testing it to verify if everything works correctly. Testing the model typically involves the following steps:
- Creating synthetic data (or retrieving real data)
- Instantiating the model
- Training the model
- Testing the model on the evaluation set
Now, we initialize a vector to represent the weights that our model needs to learn from the data during the training process, and we follow the same process for the bias. Then we compute the target that we are going to use, with the features to train our model. We can also adjust hyperparameters as needed.
# Define hyperparameters
num_samples = 4000
num_inputs = 2000
learning_rate = 0.01
epochs = 2000
batch_size = 64
# Generate synthetic data
true_w = torch.randn((num_inputs, 1))
true_b = torch.rand((1,1))
X = torch.randn((num_samples, num_inputs))
y = torch.matmul(X, true_w) + true_b + torch.randn((num_samples, 1)) * 0.01
Define hyperparameters:
- num_samples: The number of data samples to generate.
- num_inputs: The number of input features for each sample.
- learning_rate: The rate at which the model learns during training.
- epochs: The number of times the entire dataset is passed through the model during training.
- batch_size: The number of samples processed before the model’s internal parameters are updated.
Generate synthetic data:
- true_w: Randomly generated weights for the input features.
- true_b: Randomly generated bias term.
- X: Randomly generated input data with
num_samplesrows andnum_inputscolumns. - y: The target values calculated by multiplying
Xwithtrue_w, addingtrue_b, and adding a small amount of random noise to simulate real-world data.
Now we can look at the complete class with all the methods :
class LinearRegressionModel:
def __init__(self, num_inputs, learning_rate, sigma=0.01):
"""
Initialize the model parameters.
Args:
- num_inputs (int): Number of input features.
- learning_rate (float): Learning rate for gradient descent.
- sigma (float): Standard deviation for initializing weights.
"""
self.num_inputs = num_inputs
self.learning_rate = learning_rate
# Initialize weights and bias
self.w = torch.normal(mean=0.0, std=sigma, size=(num_inputs, 1), requires_grad=True)
self.b = torch.zeros(1, requires_grad=True)
self.losses = []
def forward(self, X):
"""
Compute the forward pass: y = Xw + b.
Args:
- X (torch.Tensor): Input tensor of shape (batch_size, num_inputs).
Returns:
- torch.Tensor: Predicted values of shape (batch_size, 1).
"""
return torch.matmul(X, self.w) + self.b
def compute_loss(self, y_pred, y_true):
"""
Compute Mean Squared Error loss.
Args:
- y_pred (torch.Tensor): Predicted values.
- y_true (torch.Tensor): True values.
Returns:
- torch.Tensor: Scalar loss value.
"""
return 0.5 * ((y_pred - y_true) ** 2).mean()
def update_parameters(self):
"""
Update the model parameters using gradient descent.
"""
with torch.no_grad():
self.w -= self.learning_rate * self.w.grad
self.b -= self.learning_rate * self.b.grad
# Manually zero the gradients
self.w.grad.zero_()
self.b.grad.zero_()
def train_step(self, X, y, batch_size):
"""
Perform a single training step.
Args:
- X (torch.Tensor): Input data of shape (num_samples, num_inputs).
- y (torch.Tensor): Target data of shape (num_samples, 1).
- batch_size (int): Number of samples per batch.
Returns:
- float: Loss value for the batch.
"""
# Sample a random batch
num_samples = X.shape[0]
indices = torch.randint(0, num_samples, (batch_size,))
X_batch = X[indices]
y_batch = y[indices]
# Forward pass
y_pred = self.forward(X_batch)
# Compute loss
loss = self.compute_loss(y_pred, y_batch)
# Backward pass
loss.backward()
# Update parameters
self.update_parameters()
# Return the loss value as a scalar
return loss.item()
def train(self, X, y, epochs, batch_size):
"""
Train the model over multiple epochs.
Args:
- X (torch.Tensor): Input data of shape (num_samples, num_inputs).
- y (torch.Tensor): Target data of shape (num_samples, 1).
- epochs (int): Number of training epochs.
- batch_size (int): Number of samples per batch.
Returns:
- list: List of loss values for each epoch.
"""
for epoch in range(epochs):
# Perform a training step and compute the average loss for the epoch
loss = self.train_step(X, y, batch_size)
self.losses.append(loss)
#print(loss)
print("Final Loss : ",loss)
self.plot_training_results()
#return losses
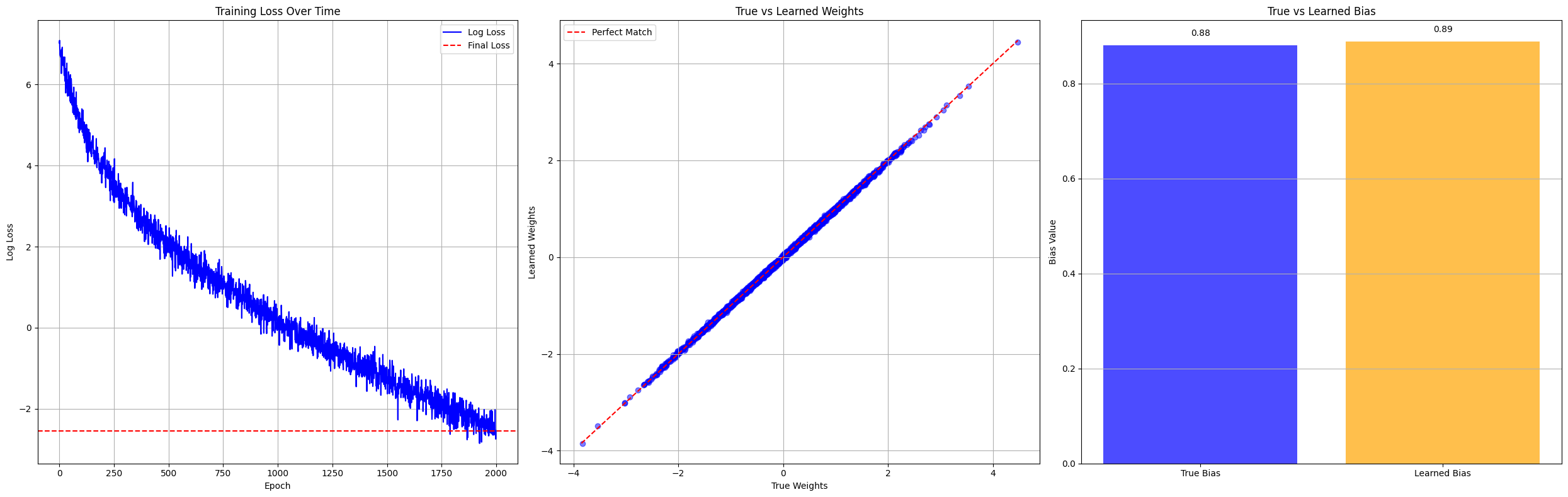
def plot_training_results(self):
plt.figure(figsize=(25, 8))
# First subplot: Training loss
plt.subplot(1, 3, 1)
plt.plot(np.log(self.losses), label="Log Loss", color="blue")
plt.axhline(np.log(self.losses[-1]), linestyle="--", color="red", label="Final Loss")
plt.xlabel('Epoch')
plt.ylabel('Log Loss')
plt.title('Training Loss Over Time')
plt.legend()
plt.grid(True)
# Second subplot: weight comparison
plt.subplot(1, 3, 2)
learned_weights = self.w.detach().numpy().flatten()
true_weights = true_w.numpy().flatten()
# Create a scatter plot comparing true vs learned weights
plt.scatter(true_weights, learned_weights, alpha=0.5, color='blue')
# Add a diagonal line representing perfect prediction
max_val = max(np.max(true_weights), np.max(learned_weights))
min_val = min(np.min(true_weights), np.min(learned_weights))
plt.plot([min_val, max_val], [min_val, max_val], 'r--', label='Perfect Match')
plt.xlabel('True Weights')
plt.ylabel('Learned Weights')
plt.title('True vs Learned Weights')
plt.legend()
plt.grid(True)
# Third subplot: Bias comparison
plt.subplot(1, 3, 3)
true_bias = float(true_b.numpy().flatten()[0])
learned_bias = float(self.b.detach().numpy().flatten()[0])
x = ['True Bias', 'Learned Bias']
y = [true_bias, learned_bias]
plt.bar(x, y, color=['blue', 'orange'], alpha=0.7)
for i, val in enumerate(y):
plt.text(i, val + 0.02, f'{val:.2f}', ha='center', fontsize=10)
plt.ylabel('Bias Value')
plt.title('True vs Learned Bias')
plt.grid(axis='y')
plt.tight_layout()
plt.show()
Model = LinearRegressionModel(num_inputs,learning_rate)
Model.train(X,y,epochs,batch_size)
Final Loss : 0.07868940383195877
Conclusion
This example, while simple, highlights some key concepts: we can view a linear regression model as a neural network, and we built this model from scratch without relying on the high-level APIs provided by PyTorch. In this second part of our machine learning series, we’ve taken a step toward higher-level abstraction. In the first post, we explored how each component of a neural network is built under the hood. Here, we leveraged PyTorch’s tensor implementation but still created the model from scratch with everything we needed to train it on our data.